You moaned and I responded. Here are just the notes for the ODU section, no questions to put you off. I will move the questions to the Learning Outcome Booklet.
Updated for the 2018 changes
Part 1, containing notes, tutorials and practicals

OUR DYNAMIC UNIVERSE 2018 word
Part 2 of the notes in word format, you can adapt these if you can open them.

These are part 2 of the notes in pdf format, so you all ought to be able to open them.
Well after spending 18 months or more several years ago putting everything together students have unanimously declared they want everything separated, so your wish is my command students- here is the complete Our Dynamic Universe section notes with nothing but the essential practicals plus one!
These are part 1 of the notes in pdf format, so you all ought to be able to open them. There is a word version underneath.
These are part 1 of the notes in word format, you can adapt these if you can open them.

New for 2022 KNOWLEDGE ORGANISERS
Teamwork by Mr Stewart (Berwickshire HS) and I. He designed and made them and I tweaked them. Thanks Mr Stewart they’re ace!


For those having trouble with Unit 1 part 1 try this little document

I’ve removed the Time Dilation detailed version and added it as a separate document as I suspect most of you wont read them; which is a pity as it makes everything seem fine! Based on Russell Stannard’s excellent book “Relativity- a very short introduction” Oxford. (2008) ISBN 978–0–19–923622–0)
ODU worked ANSWERS_4 Currently the most up to date version of the worked answers.
ODU worked ANSWERS_4 The pdf version of the most up to date version of the worked answers.
Additional Support
Chapter 1 exam questions B for CFE higher
Chapter 1 exam Answers B for CFE higher
These are powerpoints prepared for the Revised Higher in 2000. They are still relevant now, and talk through example questions. They are great for revision.


For those struggling with the vectors try these to give you some practice Great Resource from Mr Crookes. Set up your 2 vectors, either use a scale diagram or components and compare to the given answer. Enjoy!
If you don’t like proving v2=u2+2as from v=u+at then use this neat little sheet from Mr Mackenzie.
A lovely little summary from G Gibb!
Equations of Motion
4.4 ODU EqoM 2012 this document has the macros enabled (actually I think you might need to contact me to get the macros, they are not allowed to be uploaded on a WordPress Website. It allows you to check your answers for the acceleration time graphs that you drew from the velocity time graph diagrams.
using displacement equation to prove the last equation


Forces, Energy and Power
Momentum
africanfastfood This is an introduction to the momentum topic; think about the collision and where the energy is transferred.
Collisions- Think Safety before buying a car!
Gravitation
Projectiles thanks to Mr. Rossi for this one.
Battleships & AWACS Projectiles thanks to Mr. Rossi for this one too.
Special Relativity
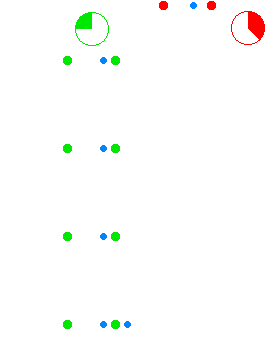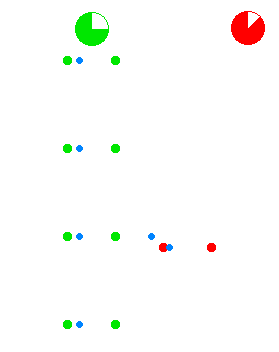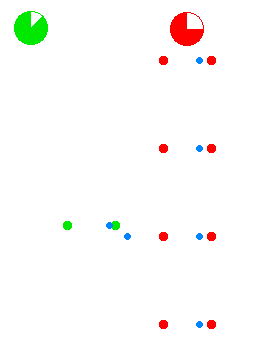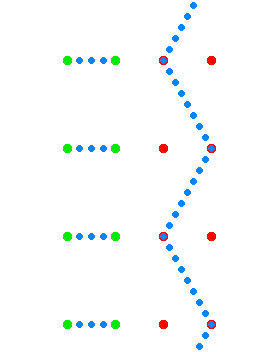
Cleonis [CC BY-SA 3.0 (http://creativecommons.org/licenses/by-sa/3.0/)]
The green dots and red dots in the animation represent spaceships. The ships of the green fleet have no velocity relative to each other, so for the clocks onboard of the individual ships, the same amount of time elapses relative to each other, and they can set up a procedure to maintain a synchronized standard fleet time. The ships of the “red fleet” are moving with a velocity of 0.866 of the speed of light with respect to the green fleet.
The blue dots represent pulses of light. One cycle of light-pulses between two green ships takes two seconds of “green time”, one second for each leg.

As seen from the perspective of the reds, the transit time of the light pulses they exchange among each other is one second of “red time” for each leg. As seen from the perspective of the greens, the red ships’ cycle of exchanging light pulses travels a diagonal path that is two light-seconds long. (As seen from the green perspective the reds travel 1.73 ({\displaystyle {\sqrt {3}}}) light-seconds of distance for every two seconds of green time.)The animation cycles between the green perspective and the red perspective, to emphasize the symmetry.
OnVelocities This is a document referred to in the Research Task in the ODU part 2 notes.
PHYSICS WORLD ARTICLE DECEMBER 2009 This is a document referred to in the Research Task in ODU part 2 notes

The Expanding Universe
The expanding universe powerpoints. Might not be quite the final version
This is the pdf version of the powerpoint
The above is the pdf version of the powerpoint
Are we missing something in the Expanding Universe?
AH (Doppler)– some of this is relevant to Higher.
HOMEWORK
The homework booklets are now in the HOMEWORK section.
Homework Booklet Complete pp6-8 (first question), 10-16, 18. Complete notes on Units prefixes and Sci Notation, Uncertainties, Equations of Motion. Read up on Forces.













 The component pushing into the slope (mg cosθ) is balanced by the reaction force from the slope.
The component pushing into the slope (mg cosθ) is balanced by the reaction force from the slope.









